¿Japonesa? ¿india? ¿china?... a saber.
Nadie sabe el por qué de su nombre, quizá sea algo japonés, quizá no. Hay quien dice que el origen de este sistema de multiplicación podría ser chino, otros que indio, el caso es que tal vez nunca lo sepamos y el origen de todo esto no sea más que otra de tantas historias nacida de los misterios de internet. Aun así, en este caso el funcionamiento de esta forma de multiplicar -algo parecido al ábaco pero con líneas y puntos- funciona y le da un toque divertido y misterioso a las matemáticas, en este caso las multiplicaciones. Veamos en que consiste.
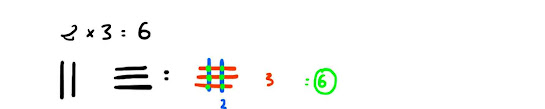
En los ejemplos de abajo efectuaremos algunas multiplicaciones simples. La primera 2x3, cuyo obvio resultado es 6.
Traduciremos 2 como dos palitos verticales, y 3 como 3 horizontales. Al representar los 2 palitos verticales, cruzados con los 3 horizontales, como vemos, hay unas intersecciones, que, marcadas con puntos verdes, al ser contadas nos dan como resultado un mágico 6.
En la siguiente multiplicación, complicaremos un poco las cosas. Efectuaremos 36x4, cuyo resultado es 144.
Para representar de esta forma un número de dos dígitos, lo haremos exactamente de la misma forma que en el caso anterior, 36 será 3 palitos verticales y otros 6 verticales también, cruzados todos ellos por 4 palitos horizontales.
En este caso al contar las intersecciones, tendremos por un lado, 12 y por otro 24. Para obtener el resultado correcto tan solo tendremos que sumar las unidades del primer número (2) con las decenas del segundo (2), con lo que obtendremos un 4, y de este modo, la cantidad de 144, que es el resultado de la multiplicación.
En el último ejemplo tendremos dos números de dos cifras. Como vimos en el caso anterior, la única mínima complicación es ir sumando bien las que se llevan a las cifras obtenidas en otras intersecciones.
En este ejemplo multiplicaremos 15x23, cuyo resultado es 345. Como vemos, representar en este caso los palitos en "rombo", nos va ser de utilidad para saber lo que tenemos que ir sumando. Nuestro 15 en líneas azules va orientado de esta forma, y el 23 en rojo, de la contraria.
Obtenemos pues en primer lugar un 2, un 3 y un 10, y finalmente un 15. Primero sumamos 3+10 (13) y a este le sumamos la decena de 15 (1), que nos dará 14. La decena de este 14 (1) se la sumaremos al 2. Una vez sumadas, desaparecen, quedando solo los resultados de las sumas.
De esta forma, obtenemos el resultado correcto de 345.
La pregunta será ahora, ¿es este sistema realmente práctico? Con toda seguridad no lo es, ya que es evidentemente mucho más lento que las multiplicaciones tradicionales con papel y boli, pero no deja de ser algo notablemente curioso y fácil de entender, para tener un punto de vista algo más interesante de las matemáticas básicas.





No hay comentarios:
Publicar un comentario